본 포스트는 '트랜스포머를 이용한 자연어 처리 - 한빛미디어'를 읽고 정리한 글입니다.
트랜스포머에 대한 글은 추후 서술하겠습니다.
쿼리(Query)
쿼리는 우리가 찾고자 하는 키를 벡터로 표현한 것입니다. 얘를 들어 메뉴판에서 고르고자 하는 메뉴가 쿼리가 됩니다.
키(Key)
키는 메뉴판에 있는 모든 메뉴를 벡터로 표현한 것입니다.
값(Value)
값은 키에 대응하는 값입니다. 예를 들면 펩시의 가격이 1500원일 때, 'Key가 펩시고 Value가 1500과 같다'라는 맥락으로 이해하시면 됩니다.
동작 방식
BERT와 같은 모델에선 각 토큰에 대해 768차원의 벡터로 매핑되어, 쿼리, 키, 값은 모두 토큰의 개수만큼의 768차원의 벡터가 모여 $(token, 768)$ 크기의 행렬로 구성됩니다.

이제, 쿼리와 키를 행렬곱을 취해줍니다.

이때, 행렬곱의 정의에 의해 $(n, m)$ $(a, b)$의 행렬곱이 정의되려면 $a=m$이라는 조건이 필요합니다.
따라서 $Key$에 전치를 취하면 $(768, token)$ 크기의 행렬이 되므로 행렬곱을 정의할 수 있게 됩니다.
$Query$는 $(token, 768)$, $Key^{T}$는 $(768, token)$의 행렬이 되므로 행렬곱의 결과는 $(token, token)$크기의 행렬이 나오게 됩니다.
근데 이 곱이 무엇을 의미하는지는 애매합니다. 이를 내적을 통해 살펴봅시다.
내적
벡터의 내적 결과는 결론적으로 두 벡터가 얼마나 닮았냐를 의미합니다.
내적을 수식적으로 정의하면 다음과 같습니다. (벡터는 볼드 처리해서 표현하겠습니다.)
$$\mathbf{a}^{T} \mathbf {b} = || \mathbf {a} || || \mathbf {b} || \cos \theta$$
이때 어떤 벡터 $\mathbf{a}$에 대해서 노름(Norm, 여기서는 L2)값을 아래와 같이 정의하고, 두 벡터의 사잇각을 $cos \theta$로 정의합니다.
$$|| \mathbf{a} || = \sqrt{\sum_{i} a_i^2}$$
이 식을 자세히 보시면, $\mathbf{a} \neq \mathbf{0}, \mathbf{b} \neq \mathbf{0}$일 때 $|| \mathbf{a} || || \mathbf{b} || > 0$인 것은 자명합니다.
따라서 우리는 $\cos \theta$에 대해서만 관찰하면 됩니다.

위 빨간선은 $y = \cos \theta$의 그래프입니다. 제가 만든 그림을 보시면
- $\theta = 0$일 때, 두 벡터의 사잇각이 $0$입니다. 따라서 두 벡터가 같은 방향을 가리킵니다.
이때는 $\cos 0 = 1$이므로 두 벡터의 내적값은 $||\mathbf{a}|| ||\mathbf{b}||$가 됩니다.
- $\theta = \frac{\pi}{2}$일 때, 두 벡터의 사잇각이 $\frac{\pi}{2}$입니다. 따라서 두 벡터가 수직을 이룹니다.
이때는 $\cos \frac{\pi}{2} = 0$이므로 두 벡터의 내적값은 $0$이 됩니다.
- $\theta = \pi$일 때, 두 벡터의 사잇각이 $\pi$입니다. 따라서 두 벡터가 서로 반대 방향을 가리킵니다.
이때는 $\cos \pi = -1$이므로 두 벡터의 내적값은 $- ||\mathbf{a}|| ||\mathbf{b}||$가 됩니다.
- $\theta = \frac{3\pi}{2}$일 때, 두 벡터의 사잇각이 $\frac{3\pi}{2}$입니다. 따라서 두 벡터가 수직을 이룹니다.
이때는 $\cos \frac{3\pi}{2} = 0$이므로 두 벡터의 내적값은 $0$이 됩니다.
따라서 두 벡터 사이의 내적값은 두 벡터의 크기와 사잇각에 따라 커지고 작아짐을 확인하실 수 있습니다.
이제 이 내적을 통해 $Query$의 각 벡터와 $Key$의 각 벡터가 얼마나 닮았는 지를 수치화해볼 수 있습니다.
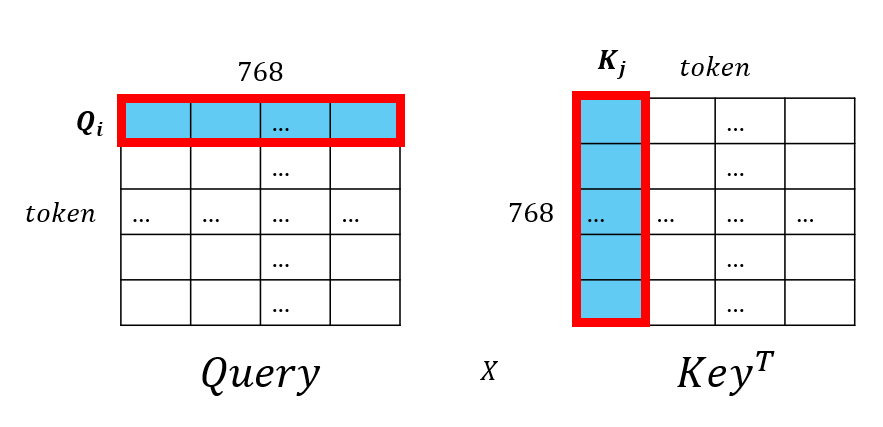
아까 봤던 그림이지만, $Query$의 $i$번째 행은 $\mathbf{Q_i}$, $Key$의 $j$번째 열을 $\mathbf{K_j}$라고 나타내면, 두 벡터의 내적 = 행렬곱 = 닮은 정도를 나타냅니다.
즉, $Query$의 $i$번째 토큰과 $Key$의 $j$번째 토큰이 벡터공간에서 얼마나 유사한지를 수치화한 값이 두 벡터의 내적이 됩니다.
이를 모든 $Query$의 $i$행, 모든 $Key^T$의 $j$열을 모두 내적을 취하게 된 결과 $Score$는 $(token, token)$의 크기로 이루어지며, $(i, j)$에 있는 값은 $Query$의 $i$번째 토큰과 $Key$의 $j$번째 토큰이 얼마나 유사한지를 나타내게 됩니다.
즉, $Score$의, $i$행에는 $Query$의 $i$번째 토큰과 $Key$의 모든 토큰과의 유사도가 어느정도인지를 알 수 있게 됩니다.
하지만, 이 값은 매우 커질 수 있기 때문에 이를 적당한 값의 범위로 맞춰주는 것이 중요합니다.
이때 이용하는 것이 스케일링(Scaling)과 소프트맥스(Softmax)입니다.
설명의 용이함을 위해 소프트맥스(Softmax)를 먼저 설명하겠습니다.
Softmax
Softmax는 아래 식을 이용해 해당 값의 범위를 $[0, 1]$로 정규화하고, 출력값의 합을 1로 맞춰주는 특성을 가지고 있습니다.
식은 아래와 같습니다.
$$ Softmax(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} $$
이를 이용해서, 위에서 구한 $Score$의 각 행에 Softmax를 적용하면 됩니다.
하지만, 위해서 구한 $Score$에 대해 $x_i$를 그대로 넣으면 문제가 생길 수 있습니다.
$x = {99, 9}$인 경우 문제를 확인할 수 있는데, $e^{99} = 9e42$와 $e^9$인 경우 $\displaystyle \frac{e^9}{e^{99} + e^9}$의 값이 아래와 같습니다.

하지만, $\displaystyle \frac{9}{99+9}$는 $0.08333...$이므로 Softmax를 사용하기에는 너무 편향되어 그냥 분수로 만드는 것이 더 나을 것 같습니다.
따라서 이를 적절히 조절하는 스케일링 단계를 통해 Softmax가 유용하게 사용될 수 있도록 하는 과정이 필요합니다.
스케일링
스케일링은 Softmax와 비슷합니다. 하지만 Softmax는 [0, 1]의 범위로 매핑한것과 달리 스케일링의 결과는 해당 범위를 벗어날 수 있습니다.
처음에 $Query$와 $Key$, 그리고 $Value$는 표준정규분포 $\mathcal{N} (0, 1)$을 따르게 초기화가 됩니다.
이때는 $Score$를 각 토큰의 차원의 크기에 제곱근을 씌운 $\sqrt{768}$로 나누어 처리해주는 과정을 거치면 최악의 경우 $e^{768 + \alpha}$을 Softmax를 적용하는 것에서 $\displaystyle e^{\frac{768 + \alpha}{\sqrt{768}}}$을 Softmax에 적용할 수 있게 됩니다.
이제 스케일링 및 Softmax를 $Score$에 적용하고 $Score$와 $Value$를 곱하게 되면 모델이 $Query$에 있는 각 단어에 대해 어떤 단어랑 같이 집중해서 봐야하는 지 알 수 있게 할 수 있습니다.
'AI' 카테고리의 다른 글
| [자연어처리] 1. 토큰화(Tokenization) (0) | 2024.09.13 |
|---|---|
| [AI - 2] 회귀의 시작 - 선형 회귀 (0) | 2024.01.25 |
| [AI - 1] 오차 함수 - 오차를 계산하자 (0) | 2024.01.20 |
